题目

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

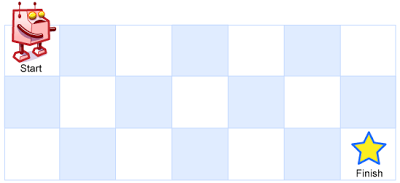
例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例 1:

1
2
3
4
5
6
7
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

1
2
输入: m = 7, n = 3
输出: 28

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10 ^ 9

题解

看到这道题第一想法是使用回溯，虽然有猜到回溯的复杂度会稍微高一些，但还是想试一下，回溯代码如下，很简单，这里不再进行详细的说明。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
void interUniquePaths(int m, int n, int x, int y, int &count) {
   if (x == m - 1 && y == n - 1) {
       count += 1;
       return;
   }

   if (x < m - 1) {
       interUniquePaths(m, n, x + 1, y, count);
   }

   if (y < n - 1) {
       interUniquePaths(m, n, x, y + 1, count);
   }
}

int uniquePaths(int m, int n) {
   int count = 0;
   interUniquePaths(m, n, 0, 0, count);
   return count;
}

提交之后，果然超时了😥，侥幸的心理果然不行。还得从动态规划的思路来考虑。

既然是动态规划，估计复杂度为O(M * N)，即遍历一遍二维数组即可得到结果。我们定义一个二维的dp数组，数组中值的含义该是什么？

我最开始想的是，当前坐标有几种可走的方法，如下图所示：

	0	1	2
0	2	2	1
1	1	1	0

在(0,0)位置处，有2种走法，在(1,0)处也有2种走法，而在(2,0)处则只有1种走法。同理在(0,1)处有1种走法，在(1,1)处依旧有1种走法，在（2，1）处到达终点。

但这种方式似乎对结果的计算没有任何帮住。我们求的是到达某个点共有几种方式，那么我们让数组种的值为到当前点共有几种方式。如下图所示：

	0	1	2
0	1	1	1
1	1	2	3

在(0,0)处，初始值为1。在(1,0)处，我们只有从左边一种方式到达，所以也为1。在(2,0)处，我们依旧只能从左边一种方式到达，那么还为1。

在(0, 1)处，我们只有上面一种方式到达，所以为值为1。而在(1,1)处，我们有上面和左边两种方式到达，那么到达方式的数量为上面与左边这两种到达方式数量之和。在(2,1)处，我们依旧有2种方式到达，分别是从上面和左边，那么总的到达方式数量为到达(2,0)与到达(1,1)这两个地方的方式之和，即为 1 + 2 = 3。我们最终求得就是(2,1)处的值，结果显然为3。

按照这种思路，我们实现代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
int uniquePaths(int m, int n) {
    int **matrix = new int*[n];
    for (int i = 0; i < n; i++) {
        matrix[i] = new int[m];
        memset(matrix[i], 0, sizeof(int) * m);
    }
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (i > 0 && j > 0) {
                matrix[i][j] = matrix[i - 1][j] + matrix[i][j - 1];
            }
            else {
                matrix[i][j] = 1;
            }
        }
    }

    return matrix[n - 1][m - 1];
}