题目
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
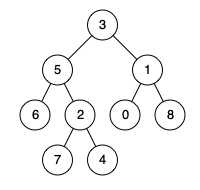
示例 1:
1
2
3
|
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
|
示例 2:
1
2
3
|
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
|
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
题解
这道题相较于二叉搜索树的最近公共祖先要稍微复杂一些,因为树不再是搜索树了,而是一颗普通的树,因此无法像上道题那样做特殊的操作。
对于这道题,最为直接的想法是根据树的根节点到p、q两个子节点路径计算出交点,这个交点便是最近的公共祖先。
下面是对应的实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q, list<pair<TreeNode*, bool>> &s, TreeNode*& f) {
if (!root)return false;
s.push_back({ root, false });
if (root->val == p->val || root->val == q->val) {
if (s.front().second) {
for (auto itr = s.rbegin(); itr != s.rend(); itr++) {
if (itr->second) {
f = itr->first;
return true;
}
}
}
else {
for (auto &itr : s) {
itr.second = true;
}
}
}
if (dfs(root->left, p, q, s, f))return true;
if (dfs(root->right, p, q, s, f)) return true;
s.pop_back();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root || !p || !q)return nullptr;
TreeNode* f = nullptr;
list<pair<TreeNode*, bool>> s;
dfs(root, p, q, s, f);
return f;
}
|
在上面的实现中,使用了链表s来保存树的路径,当找到一个节点p时,对路径进行标记。当找到另外一个节点q时,查找路径,找到最近的被标记的节点,而这个节点便是最近的公共祖先。
提交后,代码可通过,但耗时排名比较靠后,猜测实现不是最优解,遂查看了讨论,果然自己的实现复杂了,自己的那个想法是最简单的想法,但如果能对这道题做更加详细的分析后,会找到更加方便的方式。
一开始一直按照先序遍历的方式思考,但看了讨论后,发现这道题使用后续遍历会更加合适。首先对左右两个子节点进行递归判断,左子树的返回值记为left,右子树的返回值记为right。这里会分4种情况:
- 如果left和right均有返回值,说明当前的root节点便是最近的公共节点。
- 如果只有left有值,那么说明p、q的公共节点在左子树中,直接返回left。
- 如果只有right有值,那么说明p、q的公共节点在右子树中,直接返回right。
- 如果left和right都为空,那么说明右子树和左子树中都不含有公共节点,直接返回null。
递归的终止条件是,当遇到空节点时返回空,如果当前节点等于p或是等于q,那么就返回当前节点。
对应的实现如下:
1
2
3
4
5
6
7
8
9
10
11
|
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr || root == p || root == q)return root;
auto left = lowestCommonAncestor(root->left, p, q);
auto right = lowestCommonAncestor(root->right, p, q);
if (left == nullptr && right == nullptr) return nullptr;
if (left == nullptr)return right;
if (right == nullptr) return left;
return root;
}
|
上面只有3个条件,没有left和right都为空的情况,实际上这种情况被条件2、3包含了,当left为空时,会返回right,如果right也为空,那么这里返回的就是空。同理,当right为空时,如果left也为空,那么这里也返回空。
另外要注意一点,当root等于p或等于q时就直接返回了,当初看到这里自己会有疑问,那如果q是p的子节点呢?这实际上是没问题的,因为我们从下面的条件中我们可以看到当left或right不为空时直接进行返回。
