题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

1
2
3
4
5


输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例2：

1
2
3
4
5
6


输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

题解

实际上这道题跟斐波那契数列很像，用斐波那契的方法实现就成。

这道题可以倒着思考，我们考虑最终到楼梯顶时有2两种方式，即要么还有1阶到顶，要么还有2阶到顶。

那么从后往前思考，如果现在站在离顶还有1阶的地方，我们有多少种方法到这一阶？我们依旧可以将问题拆成上面那种方式思考，即有两种情况，要么走一1阶到这里，要么走2阶到这里。

如此循环下去，直到第1阶与第2阶。这些就是重叠的子问题，这里可以画一个递归树，网上盗一张图，如下。

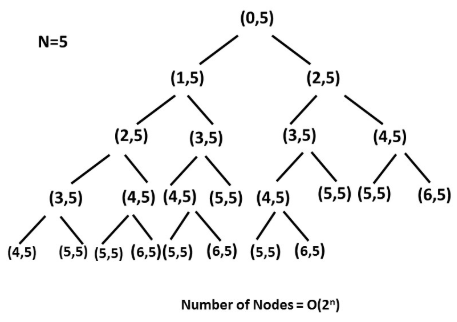
f(20)可以理解为爬到20阶楼梯的方式，有2种方式，即在19阶，再走一步到顶，或在18阶，再走2步到顶。之后再以18、19阶为基础，继续向前去问有几种方式，直到最底的1、2层。

直接实现的话，就像下面的这个代码。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


int climbStairs(int n) {
   if (n == 0) {
       return 0;
   }

   if (n == 1) {
       return 1;
   }

   if (n == 2) {
       return 2;
   }

   return climbStairs(n - 1) + climbStairs(n - 2);
}

然而在leetcode上提交后，会发现运行超时，原因在于重复的运算太多了，仔细想一下它的递归树有多大，有多少重复的计算。针对这个问题，需要对整棵树进行剪枝，降低复杂度。代码如下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


int interClimbStairs(int *data, int n) {
   if (data[n] != 0) {
       return data[n];
   }

   data[n] = interClimbStairs(data, n - 1) + interClimbStairs(data, n - 2);
   return data[n];
}

int climbStairs(int n) {
   if (n == 0) return 0;
   if (n == 1) return 1;
   if (n == 2) return 2;

   int *data = new int[n + 1];
   memset(data, 0, sizeof(int) * (n + 1));
   data[1] = 1;
   data[2] = 2;

   auto value = interClimbStairs(data, n);
   delete[] data;
   return value;
}

这里对中间运算的结果进行了存储，但耗费的内存稍微有点多，仔细考虑一下，我们的结果只依赖前面的两个状态，如果我们自底向上计算的话，只需要2个变量就够了，代码如下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


int climbStairs(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    if (n == 2) return 2;
    
    int a = 1;
    int b = 2;
    int v = 0;
    for (int i = 3; i <= n; i++) {
        v = a + b;
        a = b;
        b = v;
    }

    return v;
}

一般来说，动态规划都是自底向上计算的，当然思考时可以反过来思考，即从结果逆向思考到最开始的状态。如果使用递归逆向实现也行，只是这样的话，就需要将整个中间状态全都保存下来，稍微浪费了空间。而自底向上实现的话，只需要使用最少的中间变量即可。

补充

leetcode的题解真特么的好。